Aire d'un cercle: formule. Pourquoi l'aire d'un cercle décrite et inscrite dans un carré est-elle égale à un triangle rectangle isocèle, un trapèze rectangle isocèle?

Comment trouver l'aire d'un cercle? Trouve d'abord le rayon. Apprenez à résoudre des tâches simples et complexes.

Un cercle est une courbe fermée. Tout point sur la ligne circulaire sera équidistant du point central. Un cercle est une forme plate, donc résoudre la tâche de trouver la zone est simple. Dans cet article, nous verrons comment trouver l'aire d'un cercle inscrit dans un triangle, un trapèze, un carré, et décrit à proximité de ces figures.

Aire d'un cercle: formule utilisant rayon, diamètre, longueur d'un cercle, exemples de résolution de problèmes

Pour trouver l'aire de ​​un chiffre, vous devez savoir que tel est le rayon, le diamètre et le nombre π.

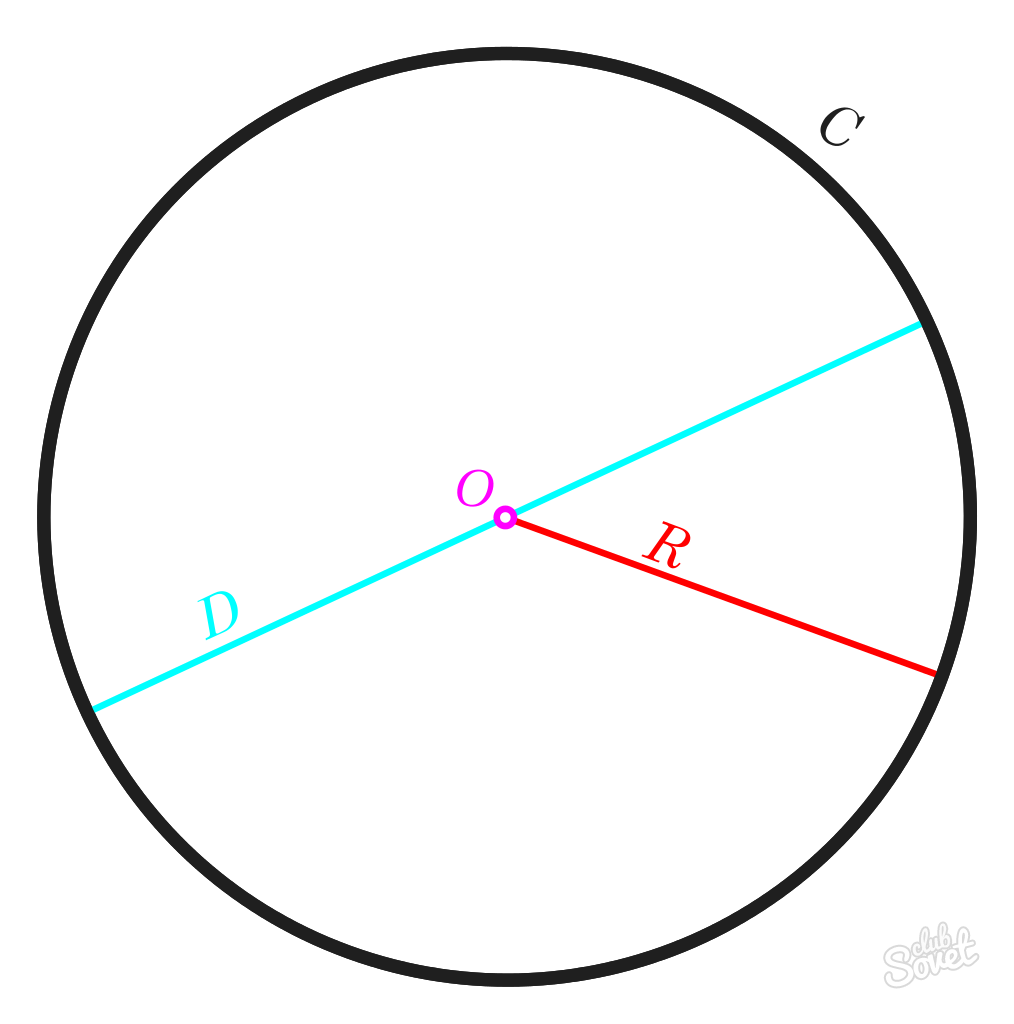
Le rayon R est la distance délimitée par le centre du cercle. Les longueurs de tous les rayons R d'un cercle seront égales.

Le diamètre D est une ligne entre deux points quelconques sur un cercle passant par le point central. La longueur de ce segment est égale à la longueur du rayon R multipliée par 2.

Le nombre π est une valeur constante égale à 3,1415926. En mathématiques, ce nombre est généralement arrondi à 3,14.

La formule pour trouver l'aire d'un cercle passant par le rayon:

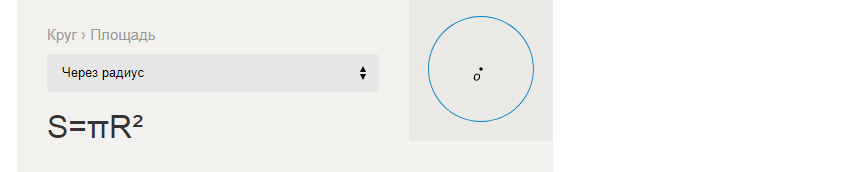
Exemples de résolution de tâches pour trouver l'aire S d'un cercle à travers le rayon R:

---------- ---------------------------- --

Tâche: Trouver l'aire d'un cercle, si son rayon est de 7 cm.

Solution: S=πR2, S=3,14*72, S=3,14*49=153,86 cm2.

Réponse: L'aire d'un cercle est de 153,86 cm2.

La formule pour trouver l'aire S d'un cercle à travers le diamètre D:

Exemples de résolution de tâches pour trouver S si D est connu:

--------- --------------------------------

Quête: Trouver S d'un cercle, si son D est égal à 10 cm.

Solution: P=π*d2/4, P=3,14*102/4=3,14*100/4=314/4=78,5 cm2.

Réponse: L'aire d'une figure ronde plate est de 78,5 cm2.

Trouver S d'un cercle, si la longueur du cercle est connue:

Premièrement, nous trouvons ce qu'est le rayon. La longueur du cercle est calculée par la formule: L=2πR, en conséquence, le rayon R sera égal à L/2π. Maintenant, nous trouvons l'aire du cercle en utilisant la formule passant par R.

Considérons la solution sur l'exemple du problème:

----------- -----------------------------

Tâche: Trouver l'aire d'un cercle, si la longueur du cercle L est connue - 12 cm.

Solution: On trouve d'abord le rayon: R=L/2π=12/2*3.14=12/6.28=1.91.

Nous trouvons maintenant l'aire passant par le rayon: S=πR2=3,14*1,912=3,14*3,65=11,46 cm2.

Réponse: L'aire d'un cercle est de 11,46 cm2.

Aire d'un cercle inscrit dans un carré: formule, exemples de résolution de problèmes

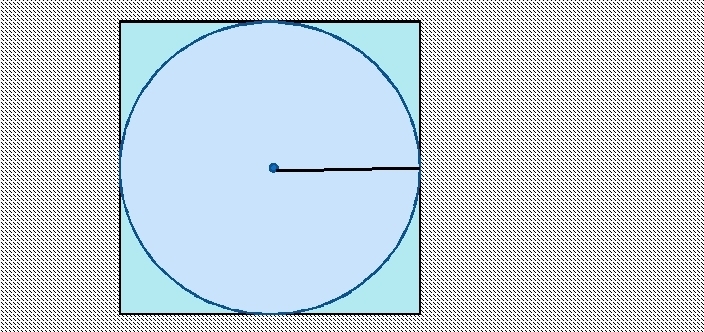
Trouver l'aire d'un cercle inscrit dans un carré est simple. Le côté du carré est le diamètre du cercle. Pour trouver le rayon, il faut diviser le côté par 2.

La formule pour trouver l'aire d'un cercle inscrit dans un carré:

Exemples de résolution de problèmes pour trouver l'aire d'un cercle inscrit dans un carré:

----------------------------------------------- ----

Tâche n° 1: Le côté d'une figure carrée, qui est égal à 6 centimètres, est connu. Trouvez la zone S du cercle inscrit.

Solution: S=π(a/2)2=3,14(6/2)2=3,14*9=28,26 cm2.

Réponse: L'aire d'une figure ronde plate est de 28,26 cm2.

----------------------------------------- -----------

Tâche #2 :Trouver S d'un cercle inscrit dans une figure carrée et son rayon si un côté est égal à a=4 voir

Résoudre comme suit : On trouve d'abord R=a/2=4/2=2 voir

Nous allons maintenant trouver l'aire du cercle S=3,14*22=3,14*4=12,56 cm2.

Réponse: L'aire d'une figure ronde plate est de 12,56 cm2.

Aire d'un cercle circonscrit à un carré: formule, exemples de résolution de problèmes

Il est un peu plus difficile de trouver l'aire d'une figure ronde décrite autour d'un carré. Mais, connaissant la formule, vous pouvez rapidement calculer cette valeur.

Formule pour trouver S d'un cercle circonscrit à une figure carrée:

Exemples de résolution de problèmes pour trouver l'aire d'un cercle décrit autour d'une figure carrée:

Problème

Aire d'un cercle inscrit dans un triangle rectangle et isocèle: formule, exemples de résolution de problèmes

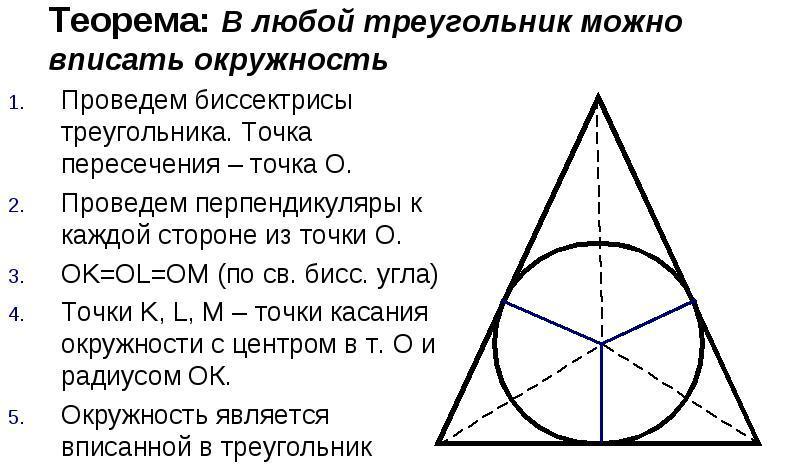
Un cercle inscrit dans une figure triangulaire est un cercle qui touche les trois côtés du triangle. Toute figure triangulaire peut être inscrite avec un cercle, mais un seul. Le centre du cercle sera le point d'intersection des bissectrices du triangle.

Formule pour trouver l'aire d'un cercle inscrit dans un triangle isocèle:

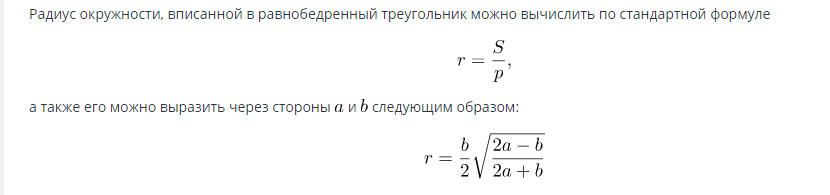
Lorsque le rayon est connu, l'aire peut être calculée par la formule: S=πR2.

Formule pour trouver l'aire d'un cercle inscrit dans un triangle rectangle:

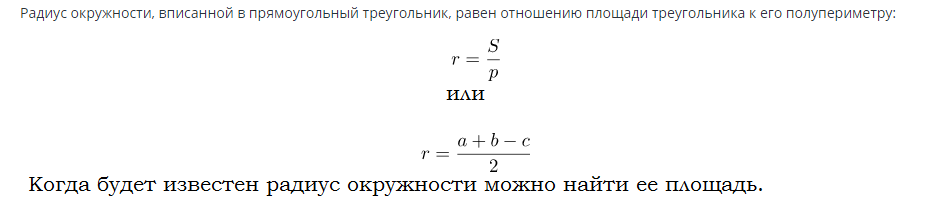
Exemples de solutions de problèmes:

Problème # 1

)

Si dans ce problème vous devez également trouver l'aire d'un cercle de rayon 4 cm, vous pouvez le faire par la formule: S=πR2

Tâche #2

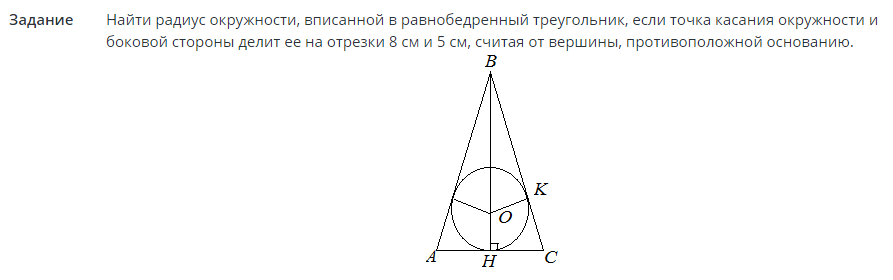
Solutions:

Maintenant que le rayon est connu, l'aire du cercle peut être trouvée en termes de rayon. Voir la formule ci-dessus dans le texte.

Tâche #3

Aire d'un cercle circonscrit à un triangle rectangle et isocèle: formule, exemples de résolution de problèmes

Toutes les formules pour trouver l'aire d'un cercle se résume au fait que vous devez d'abord trouver son rayon. Lorsque le rayon est connu, trouver la zone est simple, comme décrit ci-dessus.

​​​​

L'aire d'un cercle circonscrit à un triangle rectangle et isocèle se trouve par la formule suivante:

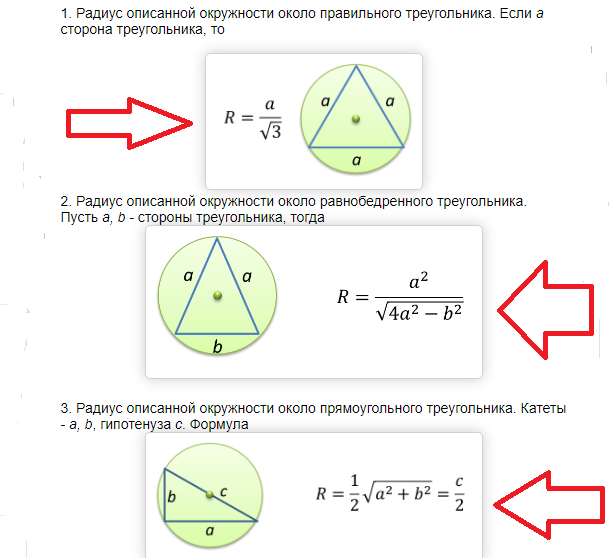
Exemples de résolution de problèmes:

Voici un autre exemple de résolution d'un problème avec la formule de Heron.

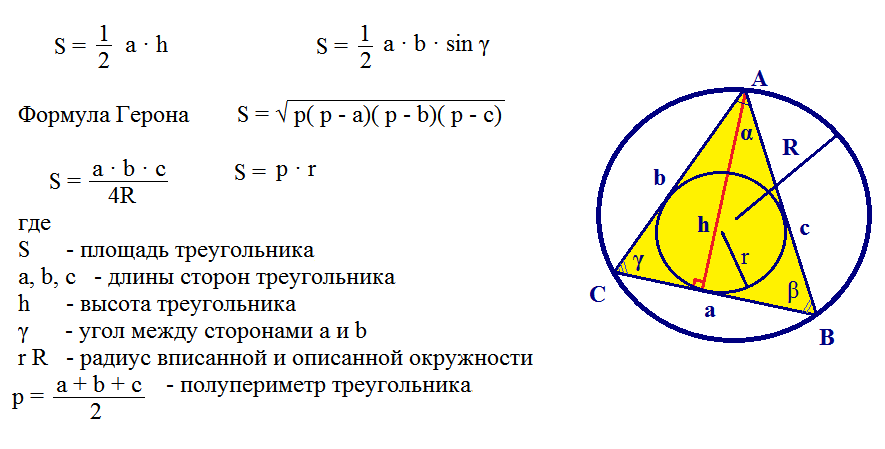
Il est difficile à résoudre problèmes similaires, mais ils peuvent être surmontés si vous connaissez toutes les formules. Les élèves résolvent de telles tâches en 9e année.

Aire d'un cercle inscrit dans un trapèze rectangle et isocèle: formule, exemples de résolution de problèmes

Par exemple, un trapèze isocèle est inscrit avec un cercle qui est au point de contact divise un côté en segments m et n.

Pour résoudre ce problème, il faut utiliser les formules suivantes:

La recherche de l'aire d'un cercle inscrit dans un trapèze rectangle s'effectue selon la formule suivante:

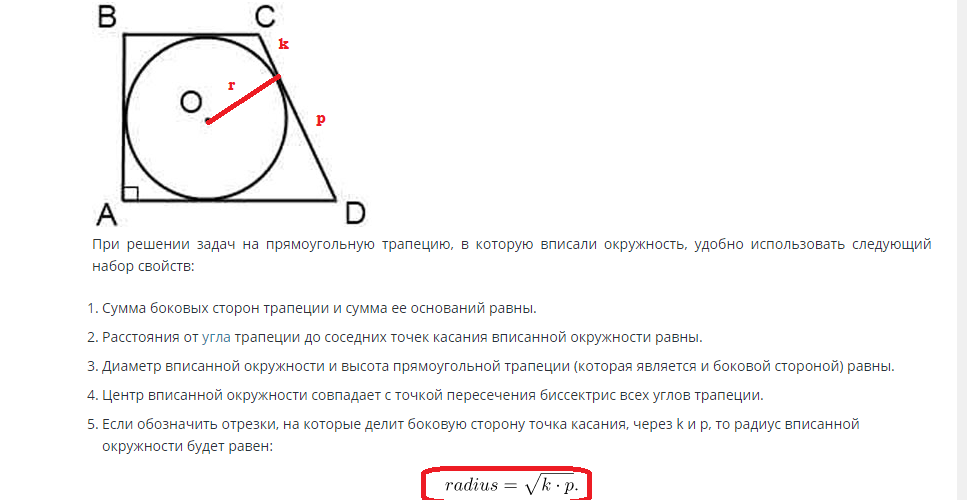
Si le côté est connu, alors le rayon peut être trouvé grâce à cette valeur. La hauteur du côté du trapèze est égale au diamètre du cercle et le rayon est la moitié du diamètre. Par conséquent, le rayon est égal à R=d/2.

Exemples de résolution de problèmes:

Aire d'un cercle circonscrit à un trapèze rectangle et isocèle: formule, exemples de résolution de problèmes

Un trapèze peut s'inscrire dans un cercle lorsque la somme des angles opposés est de 180°. Par conséquent, seul un trapèze équilatéral peut être inscrit. Le rayon de calcul de l'aire d'un cercle décrit à proximité d'un trapèze rectangle ou isocèle se calcule à l'aide des formules suivantes:

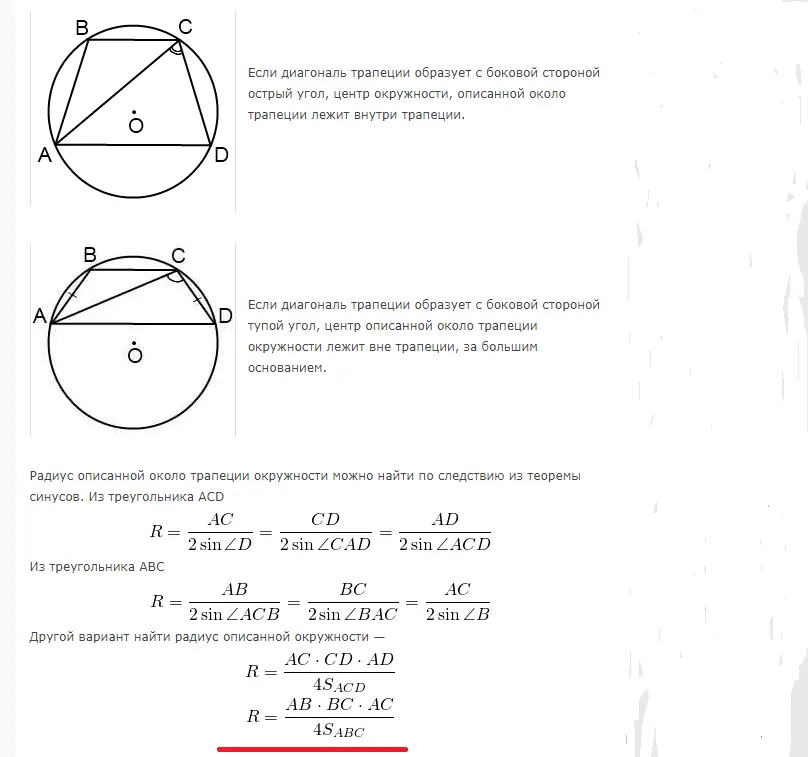
Exemples de résolution de problème:

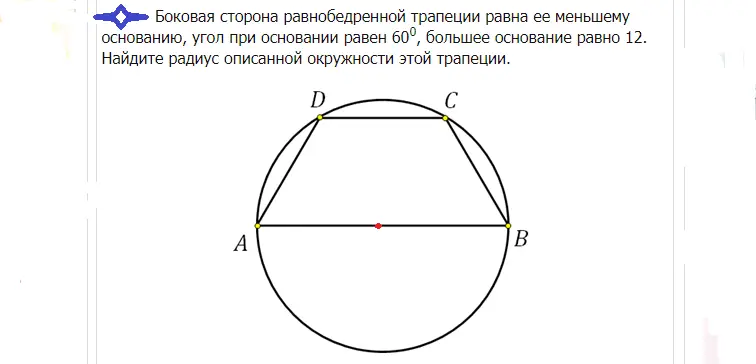
Solution: La grande base dans ce cas passe par le centre, car un trapèze isocèle est inscrit dans le cercle. Le centre divise cette base exactement en deux. Si la base AB est égale à 12, alors le rayon R peut être trouvé comme suit: R=12/2=6.

Réponse: Le rayon est 6.

En géométrie, il est important de connaître les formules. Mais il est impossible de se souvenir de tous, donc même pour de nombreux examens, il est permis d'utiliser un formulaire spécial. Cependant, il est important de pouvoir trouver la bonne formule pour la solution de tel ou tel problème. Entraînez-vous à résoudre divers problèmes pour trouver le rayon et l'aire d'un cercle afin de pouvoir remplacer correctement les formules et obtenir des réponses précises.

Vidéo: Mathématiques | Calcul des aires d'un cercle et de ses parties